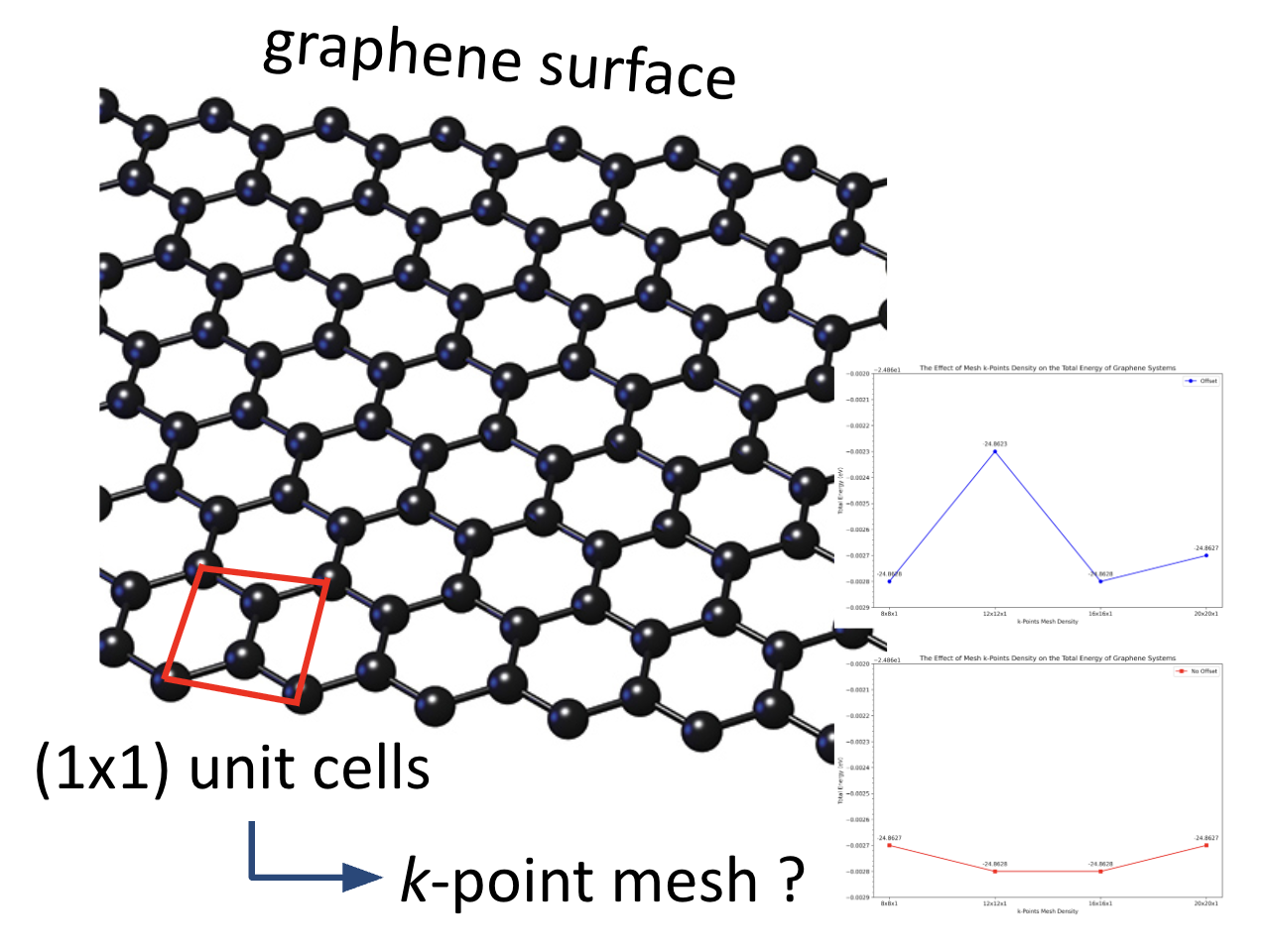
Assessing k‑Point Mesh Density for Accurate DFT Modeling (1x1) unit cell of Graphene
Main Article Content
Abstract
This study systematically evaluated the influence of k-points mesh density and offset conditions on the structural accuracy, total energy convergence, and computational efficiency of a pristine graphene system. The total energy results indicate that convergence is achieved at a k-points mesh of 12×12×1, with negligible variations up to 20×20×1. Similarly, structural parameters, including lattice constants and C–C bond lengths, demonstrate minimal deviation at higher mesh densities. However, computational time increases non-linearly with k-points density, especially under offset conditions, highlighting the trade-off between precision and computational cost. Based on a comprehensive assessment of energy stability, structural consistency, and time efficiency, the 16×16×1 no-offset k-points mesh emerges as the most balanced and reliable configuration. It yields the lowest total energy, exhibits excellent agreement with established structural benchmarks, and avoids excessive computational demand. This makes it particularly suitable as a reference system for future ab initio studies, such as H₂O adsorption on graphene, where accurate baseline energies are critical for computing adsorption energetics. The findings underscore the importance of k-points convergence testing in density functional theory (DFT) simulations and support prior literature emphasizing the balance between computational accuracy and efficiency. Future adsorption studies can confidently adopt the identified k-points mesh to ensure both reliable results and computational feasibility.
Article Details
References
[1] T. O. Wehling, A. I. Lichtenstein, M. I. Katsnelson, First- principles studies of water adsorption on graphene: The role of the substrate, Applied Physics Letters 93 (20) (2008) 202110. https://doi.org/10.1063/1.3033202.
[2] H. Khan, Cerium-Doped Titanium Dioxide (CeT) Hybrid Ma- terial, Characterization and Spiramycin Antibiotic Photocat- alytic Activity, Catalysts 15 (6) (2025) 512. https://doi.org/10.3390/catal15060512.
[3] M. Breida, S. Alami Younssi, M. Ouammou, M. Bouhria, M. Hafsi, Pollution of Water Sources from Agricultural and In- dustrial Effluents: Special Attention to NO3 , Cr(VI), and Cu(II), in: M. Eyvaz, E. Yüksel (Eds.), Water Chemistry, IntechOpen, 2020. https://doi.org/10.5772/intechopen.86921.
[4] V. I. Isaeva, M. D. Vedenyapina, A. Y. Kurmysheva, D. We- ichgrebe, R. R. Nair, N. P. T. Nguyen, L. M. Kustov, Mod- ern Carbon–Based Materials for Adsorptive Removal of Or- ganic and Inorganic Pollutants from Water and Wastewater, Molecules 26 (21) (2021) 6628. https://doi.org/10.3390/molecules26216628.
[5] I. Ali, V. K. Gupta, Advances in water treatment by adsorption technology, Nature Protocols 1 (6) (2006) 2661–2667. https://doi.org/10.1038/nprot.2006.370.
[6] C. Guan, X. Lv, Z. Han, C. Chen, Z. Xu, Q. Liu, The adsorption enhancement of graphene for fluorine and chlorine from water, Applied Surface Science 516 (2020) 146157. https://doi.org/10.1016/j.apsusc.2020.146157.
[7] R. J. Beck, Y. Zhao, H. Fong, T. J. Menkhaus, Electrospun lignin carbon nanofiber membranes with large pores for highly effi- cient adsorptive water treatment applications, Journal of Water Process Engineering 16 (2017) 240–248. https://doi.org/10.1016/j.jwpe.2017.02.002.
[8] J. Wang, J. Zhang, L. Han, J. Wang, L. Zhu, H. Zeng, Graphene- based materials for adsorptive removal of pollutants from water and underlying interaction mechanism, Advances in Colloid and Interface Science 289 (2021) 102360. https://doi.org/10.1016/j.cis.2021.102360.
[9] X. Wang, Y. Zhao, E. Tian, J. Li, Y. Ren, Graphene Oxide-Based Polymeric Membranes for Water Treatment, Advanced Mate- rials Interfaces 5 (15) (2018) 1701427. https://doi.org/10.1002/admi.201701427.
[10] N. Baig, Ihsanullah, M. Sajid, T. A. Saleh, Graphene-based adsorbents for the removal of toxic organic pollutants: A re- view, Journal of Environmental Management 244 (2019) 370–382. https://doi.org/10.1016/j.jenvman.2019.05.047.
[11] S. Kurasch, J. C. Meyer, D. Künzel, A. Groß, U. Kaiser, Simu- lation of bonding effects in HRTEM images of light element materials, Beilstein Journal of Nanotechnology 2 (2011) 394–404. https://doi.org/10.3762/bjnano.2.45.
[12] J.-L. Bretonnet, Université de Lorraine, LCP-A2MC, EA 3469, 1 Bd. François Arago, Metz, F-57078, France, Basics of the density functional theory, AIMS Materials Science 4 (6) (2017) 1372–1405. https://doi.org/10.3934/matersci.2017.6.1372.
[13] J. G. Brandenburg, A. Zen, M. Fitzner, B. Ramberger, G. Kresse, T. Tsatsoulis, A. Grüneis, A. Michaelides, D. Alfè, Physisorption of Water on Graphene: Subchemical Accuracy from Many-Body Electronic Structure Methods, The Journal of Physical Chemistry Letters 10 (3) (2019) 358–368. https://doi.org/10.1021/acs.jpclett.8b03679.
[14] J. P. Perdew, K. Burke, M. Ernzerhof, Generalized Gradient Approximation Made Simple, Physical Review Letters 77 (18) (1996) 3865–3868. https://doi.org/10.1103/PhysRevLett.77.3865.
[15] P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open- source software project for quantum simulations of materials, Journal of Physics: Condensed Matter 21 (39) (2009) 395502. https://doi.org/10.1088/0953-8984/21/39/395502.
[16] D. S. Sholl, J. A. Steckel, Density Functional The- ory: A Practical Introduction, 1st Edition, Wiley, 2009. https://doi.org/10.1002/9780470447710.
[17] X. Zou, T. Liu, Y. Li, X. Xu, A density functional theory study on thermal properties of perfect and defective graphene, Journal of Physics: Conference Series 1948 (1) (2021) 012219. https://doi.org/10.1088/1742-6596/1948/1/012219.
[18] A. Zain, Structural and Electronic Properties of Graphene upon Molecular Adsorption: DFT Comparative Analy- sis, in: J. Gong (Ed.), Graphene Simulation, InTech, 2011. https://doi.org/10.5772/20356.
[19] S. E. M. Putra, F. A. N. Habibi, D. H. Simatupang, A. Mustaqim, Adsorption and Diffusion Energies Calculation of Sodium Ion Battery using GeTe Anode : A Density Functional Theory Study, Greensusmater 1 (2) (2024) 57–62. https://doi.org/10.62755/greensusmater.2024.1.2.57-62.
[20] J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Or- dejón, D. Sánchez-Portal, The SIESTA method for ab initio order- N materials simulation, Journal of Physics: Condensed Matter 14 (11) (2002) 2745–2779. https://doi.org/10.1088/0953-8984/14/11/302.
[21] P. Mori-Sánchez, A. J. Cohen, W. Yang, Localization and De- localization Errors in Density Functional Theory and Implica- tions for Band-Gap Prediction, Physical Review Letters 100 (14) (2008) 146401. https://doi.org/10.1103/PhysRevLett.100.146401.
[22] S. Baroni, S. De Gironcoli, A. Dal Corso, P. Giannozzi, Phonons and related crystal properties from density-functional perturba- tion theory, Reviews of Modern Physics 73 (2) (2001) 515–562. https://doi.org/10.1103/RevModPhys.73.515.
[23] K. Choudhary, F. Tavazza, Convergence and machine learning predictions of Monkhorst-Pack k-points and plane-wave cut-off in high-throughput DFT calculations, Computational Materi- als Science 161 (2019) 300–308. https://doi.org/10.1016/j.commatsci.2019.02.006.